A Mindbending Scenario

Let's solve A Mindbending Scenario. This problem is a little more complicated than the previous ones, so we would do well to spend some time thinking about it before writing any code.

Initial analysis

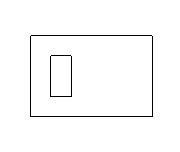
Now, what exactly is the problem statement asking? We are supplied with the coordinates of two rectangles, and asked to find the area covered between them. For example, the sample data describes two rectangles that look like this:

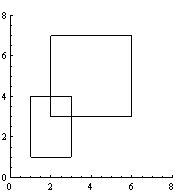
Drawing diagrams like this is useful for many reasons - it helps us to understand the problem, it helps us make sure we can read the input format correctly, and, if we are lucky, drawing diagrams may help us devise a solution.

We are told that the answer for this example is 21 (i.e. 21 unit squares are covered by the rectangles). If you wanted, you could count the squares to confirm this. In fact, let me do that for you.

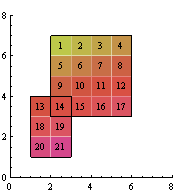
Counting the squares one by one is well and good for small cases, but according to the problem statement, co-ordinates range from 0 to 10,000. This means that for very large cases, there could be up to 100,000,000 squares to count: this is impractical to do by hand (in fact this can't be done by your typical computer within the 0.05-second time limit). Don't fret; this just means we have to find a smarter (read: faster) way of finding the area under the rectangles.

Since I've been preaching about drawing examples, let's look at some more diagrams. These showcase a variety of other possible inputs.

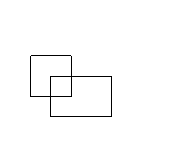
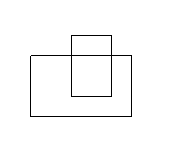
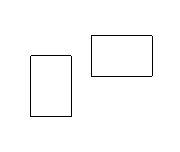
As you can see, there are many different cases our program will need to be able to deal with.

The rightmost diagram is an interesting case. Because the two rectangles are disjoint (they don't overlap), we can get the answer by adding their areas together. Recall the area of a rectangle is width times height. Your code might look something like this:

• Python 3
• C++

area = (right - left) * (top - bottom)

area = (right - left) * (top - bottom);

Of course, you'll need to do this for both rectangles. (Also, you'll want to use variable names that make sense to you. Make sure you read the input variables in the correct order - using these names it would be left, bottom, right, top.)

From this we can see how to write a program that gives the correct answer if the two rectangles don't overlap. If you're really itching to start typing, you could try coding that up. However, as you can probably guess it doesn't give correct answers most of the time, and so it's barely worth the trouble. Let's wait until we have a better idea what to do before heading for the keyboard.

What's so bad about adding the two areas together? If we try that approach for the sample data, we get an answer of 2x3 + 4x4 = 22, which is greater than the correct answer.

Trying this on the other examples gives us similar results: we consistently get numbers that are greater than the actual answer. But the problem is much more specific than that:

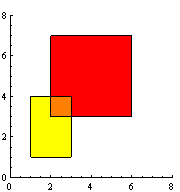
The above diagram is the sample data again, but with added shading. When we add the two rectangle areas together, we account for all the coloured areas correctly. However, the orange area will be counted twice - once when we add the area of the first rectangle and once when we add the area of the second. Our current method overshoots by exactly the area of the overlap.

This observation leads us to the following idea:

Now that we have a formula which guarantees us the correct answer every time, we have a rough idea of what our program needs to do.

• Read in the co-ordinates of the rectangles from bendin.txt.
• Calculate the area covered:
  • Calculate the area of the invididual rectangles.
  • Calculate the co-ordinates of their overlap (if any).
  • Calculate the area of their overlap (if any).
• Write the answer to bendout.txt.

Now, calculating the area of the rectangles (and their overlap, which will also be rectangular) is done using the width-by-height formula discussed above. We'll jump straight to the interesting part, which is working out the co-ordinates of the intersection rectangle.

Finding the rectangle of intersection

To reiterate, we're trying to find the co-ordinates of the intersection so that we can calculate its area, using something like the (right-left)*(top-bottom) formula mentioned before.

Knowing this, it makes sense to try to work out left_intr, right_intr and so on before we do that calculation. (Again, I'm using my own variable names: left_intr gives me the x-value for the left edge of the intersection, and so on.) Somehow we have to take the input co-ordinates and convert them into the overlap co-ordinates, however it is not immediately clear how to do this.

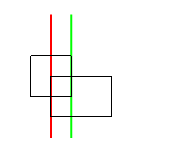
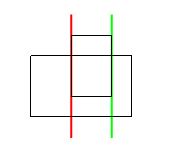
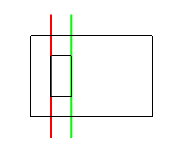
Again, when we're not sure what to do, it's often useful to draw diagrams and experiment with examples. I've taken some examples from before and used coloured lines to show the values of left_intr and right_intr.

Let's just worry about the red lines right now - these correspond to left_intr. What can we observe about their positions?

Notice how in each of the examples, the red line coincides with one of the rectangles' edges. Intuitively, this makes sense; we would expect the intersection to share borders with the original shapes. In fact, we can be more specific and say that the red line coincides with one of the rectangles' left edges. That is, left_intr is either left_1 or left_2.

We've narrowed it down to two choices, but how do we know which of the left edges to pick? In fact the answer is quite straightforward: we have to pick the one further to the right. This works in the above examples, and if you experiment a little you'll see why the leftmost edge can't possibly be part of the intersection (unless both left edges are the same, but then it doesn't matter which one we pick).

We have something tangible to code now: to find out left_intr, we look at left_1 and left_2 and pick which one is further to the right (i.e. the greater x-value). We can use if statements to do this:

• Python 3
• C++

if left_1 > left_2:
	left_intr = left_1 # left_1 is further right
else:
	left_intr = left_2 # choose the other one

if (left_1 > left_2) {
	left_intr = left_1; //left_1 is further right
} else {
	left_intr = left_2; //choose the other one
}

(There are other ways of picking the greatest of two variables, but this way uses only techniques we've already seen. I encourage you to investigate alternatives and see if you find them easier to code/understand.)

One down, three to go. Let's give right_intr a shot.

We observe something similar to before: the green line always coincides with one of the rectangles' right edges. In fact, it's always the one further to the left (i.e. the smaller x-value). This suggests some code:

• Python 3
• C++

if right_1 < right_2:
	right_intr = right_1 # right_1 is further left
} else {
	right_intr = right_2 # choose the other one
}

if (right_1 < right_2) {
	right_intr = right_1; // right_1 is further left
} else {
	right_intr = right_2; // choose the other one
}

Now, I won't spell it out for you, but bottom_intr and top_intr can be calculated in a similar way. Play around with some diagrams and see if you can work it out. Once we have all four values we can easily find the area of the intersection:

• Python 3
• C++

area_intr = (right_intr - left_intr) * (top_intr - bottom_intr)

area_intr = (right_intr - left_intr) * (top_intr - bottom_intr);

Shrewd readers may have noticed I've glossed over an important assumption. Everything I've said about calculating the co-ordinates of the intersection rectangle only works if there is an intersection to speak of. If there isn't an intersection, then area_intr should be zero and our program will still get the wrong answer.

Don't panic; we can address this with just a little extra code. Observe that if the rectangles don't intersect, then either one is to the right of the other, one is above the other, or both. The following diagram shows what happens in the first of these cases. Go ahead and draw the second of these cases on paper.

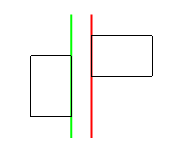
As it is, our program sets left_intr (the red line) to the rightmost left edge, and right_intr (the green line) to the leftmost right edge. Because the rectangles don't overlap horizontally, we have somehow ended up with left_intr > right_intr, which makes no sense. (Similarly, bottom_intr > top_intr when they don't overlap vertically.)

If there is no overlap, our intersection rectangle makes no sense. This means that if our intersection rectangle does make sense, then there is definitely an overlap and we have nothing to worry about. A slight modification to our code accounts for this:

• Python 3
• C++

# The only unfamiliar thing here is the keyword "and". This is the logical "and" operator, which takes two expressions
# and tells you whether they are both true. It still makes sense when read aloud:
# "If left is less than right, and bottom is less than top..."
if left_intr < right_intr and bottom_intr < top_intr:
	# if the x-coordinates make sense and the y-coordinates make sense...
	area_intr = (right_intr - left_intr) * (top_intr - bottom_intr) # they overlap, so calculate the area
else:
	area_intr = 0 # there's no overlap

// The only unfamiliar thing here is the &&. This is the logical "and" operator, which takes two expressions
// and tells you whether they are both true. It still makes sense when read aloud:
// "If left is less than right, and bottom is less than top..."
if (left_intr < right_intr && bottom_intr < top_intr) {
	// if the x-coordinates make sense and the y-coordinates make sense...
	area_intr = (right_intr - left_intr) * (top_intr - bottom_intr); // they overlap, so calculate the area
} else {
	area_intr = 0; // there's no overlap
}

We've covered all cases; our program should now calculate area_intr properly no matter what the input is.

Calculating the overall area

The areas of the 'normal' rectangles, area_1 and area_2, are straightforward to calculate. Once we have all three partial areas, we can use the formula introduced earlier:

• Python 3
• C++

area_total = area_1 + area_2 - area_intr

area_total = area_1 + area_2 - area_intr;

At this point it's just housekeeping (writing the answer to file, closing our files, and so on). In other words, you should now be able to code up a solution to A Mindbending Scenario! I can't pat you on the back, but feel free to do it yourself.